Introducción A Los Cuerpos Geométricos Y Sus Características: ¡Prepárate para un viaje fascinante al mundo de las formas geométricas! Desde los imponentes prismas hasta las elegantes esferas, exploraremos las características de estos cuerpos, desentrañando sus secretos y descubriendo su presencia en nuestro día a día. ¿Alguna vez te has preguntado cómo se calcula el volumen de una pirámide o la superficie de un cilindro?
Pues bien, ¡este es tu momento para descubrirlo! Acompáñame en esta aventura geométrica donde la diversión y el aprendizaje se dan la mano.
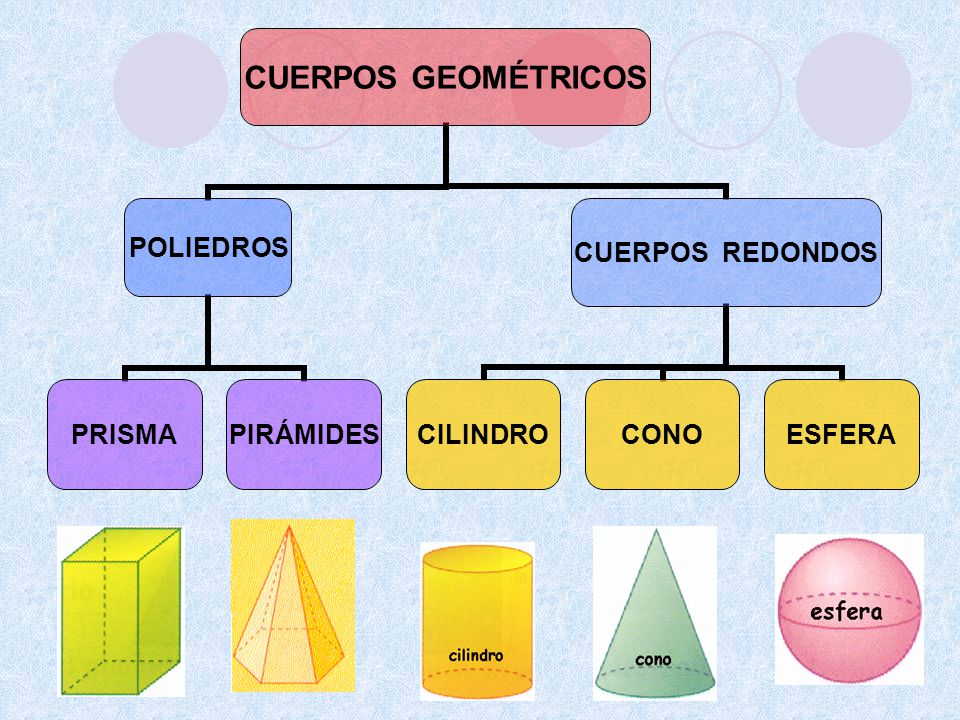
Vamos a adentrarnos en el apasionante mundo de los cuerpos geométricos, clasificándolos en poliedros (como prismas y pirámides) y cuerpos redondos (cilindros, conos y esferas). Veremos cómo se diferencian, qué elementos los componen (caras, aristas, vértices, radio, altura…), y cómo calcular sus áreas y volúmenes. Además, exploraremos sus aplicaciones prácticas en la arquitectura, la ingeniería y ¡hasta en objetos cotidianos que te rodean! Prepárate para ejercitar tu visión espacial y descubrir la geometría que nos envuelve.
Introducción a los Cuerpos Geométricos: Introducción A Los Cuerpos Geométricos Y Sus Características
¡Prepárate para un viaje fascinante al mundo de las formas geométricas tridimensionales! En este recorrido, exploraremos los cuerpos geométricos, desde sus definiciones básicas hasta sus aplicaciones en la vida real. Descubriremos cómo se clasifican, sus características únicas, y cómo podemos visualizarlos y representarlos. ¡Comencemos!
Definición y Clasificación de Cuerpos Geométricos

Los cuerpos geométricos son figuras tridimensionales que ocupan un lugar en el espacio. Se caracterizan por tener volumen, superficie y diferentes elementos como caras, aristas y vértices. Se clasifican principalmente en dos grandes grupos: poliedros y cuerpos redondos.
Los poliedros son cuerpos geométricos cuyas caras son polígonos planos. Ejemplos comunes incluyen cubos, prismas y pirámides. Por otro lado, los cuerpos redondos presentan al menos una superficie curva. Cilindros, conos y esferas son ejemplos clásicos de esta categoría.
| Tipo | Características | Ejemplos | Diferencias Clave |
|---|---|---|---|
| Poliedros | Caras planas, aristas rectas, vértices. | Cubo, prisma triangular, pirámide cuadrada. | Todas las caras son planas. |
| Cuerpos Redondos | Al menos una superficie curva, radio, diámetro, altura (en algunos casos). | Cilindro, cono, esfera. | Presentan al menos una superficie curva. |
Poliedros: Prismas y Pirámides
Los prismas y las pirámides son dos tipos importantes de poliedros. Un prisma es un poliedro con dos bases congruentes y paralelas, conectadas por caras laterales que son paralelogramos. Una pirámide, por otro lado, tiene una base poligonal y caras laterales triangulares que se unen en un vértice común llamado ápice.
Los prismas pueden ser rectos (las caras laterales son rectángulos) u oblicuos (las caras laterales son paralelogramos no rectangulares). Similarmente, las pirámides pueden ser regulares (la base es un polígono regular y la altura pasa por el centro de la base) o irregulares.
Ilustración de un prisma triangular: Imaginemos un triángulo equilátero como base, y tres rectángulos como caras laterales, uniéndose para formar dos bases triangulares paralelas. Cada rectángulo conecta un lado del triángulo de la base con su correspondiente en la base superior. Los vértices son los tres vértices de cada base triangular y los tres puntos donde se unen los rectángulos. Las aristas son los tres lados de cada triángulo y los tres lados de cada rectángulo que conectan las bases.
Ilustración de una pirámide cuadrangular: Visualicemos un cuadrado como base, y cuatro triángulos isosceles como caras laterales que convergen en un punto superior, el ápice. Los vértices son los cuatro vértices del cuadrado y el ápice. Las aristas son los cuatro lados del cuadrado y los cuatro lados de cada triángulo que conectan la base con el ápice.
- Prisma triangular: Tres caras laterales rectangulares, dos bases triangulares.
- Prisma cuadrangular (o paralelepípedo): Cuatro caras laterales rectangulares, dos bases cuadradas.
- Prisma pentagonal: Cinco caras laterales rectangulares, dos bases pentagonales.
- Y así sucesivamente, con el número de lados de la base determinando el número de caras laterales.
Cuerpos Redondos: Cilindros, Conos y Esferas

Los cuerpos redondos se caracterizan por la presencia de superficies curvas. Un cilindro tiene dos bases circulares congruentes y paralelas unidas por una superficie curva. Un cono posee una base circular y una superficie curva que se estrecha hasta un punto llamado vértice o ápice. Una esfera es un cuerpo redondo perfectamente simétrico, con todos sus puntos equidistantes de un punto central llamado centro.
Un cilindro, cono y esfera comparten elementos como el radio y el diámetro (en las bases circulares, si los tienen), pero se diferencian en su forma y propiedades geométricas. La altura es un elemento clave en cilindros y conos, mientras que la generatriz es la distancia entre el vértice y un punto de la circunferencia de la base en el cono.
| Cuerpo Geométrico | Fórmula del Área | Fórmula del Volumen |
|---|---|---|
| Cilindro | 2πr² + 2πrh | πr²h |
| Cono | πr² + πr√(r² + h²) | (1/3)πr²h |
| Esfera | 4πr² | (4/3)πr³ |
El área superficial de un cuerpo redondo representa la superficie total que lo recubre, mientras que el volumen indica la cantidad de espacio que ocupa en tres dimensiones.
Aplicaciones de los Cuerpos Geométricos en la Vida Real
Los cuerpos geométricos están presentes en innumerables objetos de nuestro entorno. Desde la forma de una lata de refresco (cilindro) hasta la estructura de una pirámide (pirámide), las formas geométricas son fundamentales en el diseño y la construcción.
- Una pelota de fútbol (esfera).
- Una caja de zapatos (prisma rectangular).
- Un cono de helado (cono).
- Una lata de sopa (cilindro).
- Una pirámide en Egipto (pirámide).
El cálculo del área y el volumen es crucial en aplicaciones prácticas, como determinar la cantidad de pintura necesaria para pintar una pared (área) o el volumen de agua que cabe en un tanque cilíndrico (volumen). En arquitectura e ingeniería, el conocimiento de los cuerpos geométricos es esencial para el diseño de estructuras estables y eficientes. Por ejemplo, la forma de un domo geodésico se basa en la estructura de un icosaedro, maximizando la resistencia con el mínimo material.
- Edificios con formas cúbicas o prismáticas para espacios habitacionales.
- Domes geodésicos para cubiertas de estadios y estructuras de gran envergadura.
- Torres con formas cilíndricas para optimizar la resistencia al viento.
- Pirámides para estructuras monumentales y con fines simbólicos.
- Conos en el diseño de silos de almacenamiento.
Desarrollo de Habilidades de Visualización Espacial, Introducción A Los Cuerpos Geométricos Y Sus Características
La visualización espacial es la capacidad de mentalmente manipular y rotar objetos tridimensionales en el espacio. Es fundamental para comprender la geometría y resolver problemas relacionados con los cuerpos geométricos. Un buen desarrollo de esta habilidad facilita la comprensión de las relaciones espaciales entre las diferentes partes de un cuerpo geométrico.
Actividades como construir modelos de cuerpos geométricos con materiales como plastilina o papel, usar software de modelado 3D, o incluso jugar con rompecabezas espaciales, ayudan a desarrollar la visualización espacial. Representar cuerpos geométricos en dos dimensiones requiere dibujar vistas desde diferentes perspectivas (vista frontal, lateral y superior).
Construcción de un cubo a partir de una plantilla:
- Obtener una plantilla de un cubo, que es un cuadrado con solapas para pegar.
- Doblar cuidadosamente las líneas de la plantilla para formar las caras del cubo.
- Aplicar pegamento a las solapas.
- Unir las solapas para formar un cubo sólido.
¡Y así concluye nuestro emocionante recorrido por el universo de los cuerpos geométricos! Hemos desentrañado sus misterios, desde la definición de cada forma hasta sus aplicaciones en el mundo real. Ahora, con una nueva perspectiva geométrica, podrás apreciar la belleza y la funcionalidad de estas figuras en tu entorno. Recuerda que la geometría no es solo una materia de estudio, sino una herramienta poderosa para comprender y transformar el mundo que nos rodea.
¡Sigue explorando, sigue aprendiendo, sigue creando!
